- (valores característicos y vectores característicos)
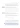
- (def 1: valor característico y vector característico)
- (ejm 1: valores característico y vectores característica de una matriz de 2x2)
- (ejm 2: valores característico y vectores característica de la matriz identidad)
- (teorema 1: λ es un valor característico de A ⟺ p(λ) = |A−λI| = 0 )
- (def 2: ecuación y polinomio característico)
- (teorema 2)
- (def 3: espacio característico)
- (teorema 3: los vectores característicos correspondientes a valores característicos distintos son l.i. )
- (multiplicadad algebraica)
- (ejm 3: cálculo de valores y vectores característicos)
- (ejm 4: una matriz de 3x3 con valores característicos distintos)
//
- (ejm 5: una matriz de 2x2 con uno de sus valores característicos iguales a cero)
- (ejm 6: una matriz de 2x2 con valores característicos conjugados complejos)
- (teorema 4)
- (ejm 7: valores característico de una matriz triangular)
- (ejm 8: una matriz de 2x2 con valor característico y dos vectores característicos linealmente independientes)
//
- (ejm 9: una matriz de 2x2 con un valor característico y solo un vector característico independiente)
- (ejm 10: una matriz de 3x3 con dos valores característicos y tres vectores característicos linealmente independientes)
- (ejm 11: una matriz de 3x3 con un valor característico y solo un vector característico independiente)
- (ejm 12: una matriz de 3x3 con un valor característico y solo un vector característico independiente)
- (def 4: multiplicidad geométrica)
- (teorema 5, 6, 7)
- (autoevaluación)
- (un modelo de crecimiento de población)
- (ejm 1: una ilustración del modelo aplicado durante 20 generaciones)
- (ejm 1: los valores y vectores característicos de A determinan el comportamiento de generaciones futuras)
- (matrices semejantes y diagonalización)
- (def 1: matrices semejantes)
- (ejm 1: dos matrices semejantes)
- (ejm 2: una matriz semejante a una matriz diagonal)
//
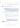
- (teorema 1: si A∼B ⟹ det(A−λI) = det(B−λI) )
- (ejm 3: los valores característicos de matrices semejantes son los mismos)
- (def 2: matriz diagonalizable: An es diagonizable ⟺ existe D tal que A∼D )
- (teorema 2: D = C-1AC )
- (corolario: Anxn tiene n valores característicos ⟹ A es diagonizable )
- (ejm 4: diagonalización de una matriz 2x2)
- (ejm 5: diagonalización de una matriz 3x3 con tres valores característicos distintos)
- (ejm 6: diagonalización de una matriz 3x3 con dos valores característicos distintos y tres vectores característicos linealmente independiente)
//
- (ejm 7: una matriz de 2x2 con solo un vector característico linealmente independiente que no se puede diagonalizar)
- (teorema 3: A=|T|B1 y B=|T|B2 ⟹ A∼B )
- (matrices simétricas y diagonalización ortogonal)
- (teorema 1: A ∈ ℝnxn es simétrica ⟹ λi ∈ ℝ )
- (teorema 2: A es simétrica y λ1 ≠ λ2 ⟹ v1 y v2 son ortogonales )
- (teorema 3: Anxn es simétrica ⟹ A tiene n vectores ortogonales )
- (def 1: A es matriz diagonizable ortogonalmente ⟺ QTAQ=D )
- (teorema 4: A es diagonizable ortogonalmente ⟺ A es simétrica )
- (ejm 1: diagonalización de una matriz simétrica de 2x2 usando una matriz ortogonal)
- (ejm 2: diagonalización de una matriz simétrica de 3x3 usando una matriz ortogonal)
- (transpuesta conjugada, matriz hermitiana, matriz unitaria)
- (formas cuadráticas y secciones cónicas)
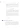
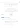
- (def 1: ecuación y forma cuadrática)
- (ejm 1: expresión de una forma cuadrática en las nuevas variables x' y y' sin término x'y')
- (teorema 1: teorema de los ejes principales en R2)
- (ejm 2: identificación de una hiperbola)
- (ejm 3: una eclipse)
- (ejm 4: una sección cónica degenerada)
- (ejm 5: eclipsoide)
- (ejm 6: una forma cuadrática en cuatro variables)
- (forma canónica de Jordan)
- (matriz de bloques de Jordan)
- (matriz de Jordan)
- (ejm 1: tres matrices de Jordan)
- (ejm 2: matrices de Jordan 2x2)
- (ejm 3: matrices de Jordan 3x3)
- (teorema 1)
- (def 1: forma canónica de Jordan)
- (teorema 2)
- (def 2: vector característico generalizado)
- (ejm 4: vector característico generalizado)
- (teorema 3)
- (ejm 5: forma canónica de Jordan de una matriz 2x2)
- (ejm 6: determinación de las posibles formas canónicas de Jordan de una matriz de 4x4 con ecuación característica dada)
- (una aplicación importante: forma matricial de ecuaciones diferenciales)
- (cálculo)
- (ecuación diferencial)
- (valor inicial)
- (función vectorial)
- (def 1: la matriz eA)
- (norma de una matriz)
- (teorema 1)
- (def 2: matriz solución principal)
- (ejm 1: cálculo de eAt cuando A es una matriz diagonal)
- (ejm 2: cálculo de eAt cuando A es una matri de 2x2 que no es diagonizable)
- (teorema 2)
- (ejm 3: un modelo competitivo)
- (ejm 4: un modelo depredador-presa)
- (ejm 5: otro modelo depredador-presa)
- (ejm 6: modelo de cooperación de especies (simbiosis))
- (una perspectiva diferente: los teoremas de Cayley-Hamilton y Gershgorin)
- (ejm 1: evaluación de p(a))
//
- (teorema 1)
- (teorema 2: teorema de Cayley:Hamilton)
- (ejm 2: ilustraión del teorema de Cayley-Hamilton)
- (ejm 3: aplicación del teorema de Cayley-Hamilton para calcular A-1 )
- (teorema de las circunferencias de Gershgorin)
- (teorema 3: )
- (ejm 4: uso del teorema de Gershgorin)
- (resumen)
- (ejercicios de repaso)
(valores característicos y vectores característicos)(autoevaluación)
(manejo de la calculadora)
(un modelo de crecimiento de población)(matlab)
(matrices semejantes y diagonalización)(autoevaluación)
(matrices simétricas y diagonalización ortogonal)(autoevaluación)
(formas cuadráticas y secciones cónicas)(autoevaluación)
(forma canónica de Jordan)(autoevaluación)
(una aplicación importante: forma matricial de ecuaciones diferenciales)(autoevaluación)
(una perspectiva diferente: los teoremas de Cayley-Hamilton y Gershgorin)(autoevaluación)
(resumen)(ejercicios de repaso)
(apéndice 1: inducción matemática)
(apéndice 2: números complejos)
(apéndice 3: el error numérico en los cálculos y la complejidad computacional)
(apéndice 4: eliminación gaussiana con pivoteo)
(apéndice 5: uso de matlab)
(autoevaluación)
(manejo de la calculadora)
(un modelo de crecimiento de población)
(matlab)
(matrices semejantes y diagonalización)
(autoevaluación)
(matrices simétricas y diagonalización ortogonal)
(autoevaluación)
(formas cuadráticas y secciones cónicas)
(autoevaluación)
(forma canónica de Jordan)
(autoevaluación)
(una aplicación importante: forma matricial de ecuaciones diferenciales)
(autoevaluación)
(una perspectiva diferente: los teoremas de Cayley-Hamilton y Gershgorin)
(autoevaluación)
(resumen)
(ejercicios de repaso)
(apéndice 1: inducción matemática)
(apéndice 2: números complejos)
(apéndice 3: el error numérico en los cálculos y la complejidad computacional)
(apéndice 4: eliminación gaussiana con pivoteo)
(apéndice 5: uso de matlab)
No hay comentarios.:
Publicar un comentario