Yachakaj: FORMA CANÓNICA DE JORDAN

miércoles, 7 de junio de 2023

FORMA CANÓNICA DE JORDAN

(diagonalización)

(def 1: matrices semejantes: A∼B ⟺ A = C.B.C^-1 )
(proposición 2: A∼B ⟺ ∃ f una TL , |f|_B₁ = A y |f|_B₂ = B )
(def 3: matriz diagonizable)
(def 4: transformación lineal diagonizable)
(proposición 5: f es diagonizable ⟺ |f|_B es diagonizable )

(autovalores y autovectores)

(obs 6)
(def 7: autovector de una TL)
(proposición 8: f es diagonizable ⟺ existe una base B formada por autovectores de f )
(obs 9: autovector ⟺ vector propio ⟺ vector característico ||| autovalor ⟺ valor propio ⟺ valor característico )
(ejm 10)
(obs 11)
(proposición 12: los autovectores asociados a autovalores distintos son l.i. )
(def 13: autovector de una matriz)
(proposición 14: A es diagonizable ⟺ existe una base de K_n formada por autovectores de A )
(proposición 15: λ autorvalor de f ⟺ f−λI no es inversible )
(ejm 16)

(polinomio característico)

(def 17: polinomio característico de una matriz ; χ_f = p(x) = det(xI-A) )
(ejm 18)
(obs 19)
(proposición 20: λ autovalor de A ⟺ λ es una raiz de p(A) )
(ejm 21)

(polinomio característico de un endomorfismo)

(proposición 22: dos matrices semejantes tienen el mismo polinomio característico)
(obs 23: la recíproca no es verdad, dos matrices pueden tener el mismo polin. caract. y no ser semejantes)
(def 24: polinomio característico de un endomorfismo ; notación: χ_f )
(proposición 25: λ es un autovalor de f ⟺ λ es raíz de χ_f )

(una caracterización de matrices diagonizables)
(suma directa de un número fínito de subespacios)

(def 26: suma de espacios)
(def 27: suma directa de subespacios)
(proposición 28, 29)

(espacios de autovectores y diagonalización)

(def 30: autoespacio ; notación: E_λ )
(proposición 31: E_λ₁ , ... , E_{λ_n} estan en suma directa)
(proposición 32: siempre existe una relación entre E_λ y la multiplicidad de λ como raíz de χ_A )

(¿cuales son las condiciones suficientes y necesarias sobre los subespacios E_λ, asociados a los autovalores λ de A, para que A sea diagonizable?)

(teorema 33)
(ejm 34: decidir si la matriz es diagoniable)

(polinomio minimales)

(def 35: especialización de x por A ; P(A) )
(ejm 36)
(obs 37)
(def 38: P(T) )
(lema 39: para cualquier matriz existe un polinomio no nulo que la anula)
(proposición 40: para toda matriz existe un único polinomio de grado mínimo y mónico que lo anula )
(def 41: polinomio minimal de A; notación: m_A )
(ejm 42)//
(proposición 43: el conjunto de polinomios que anulan a la matriz pueden caracterizarse a partir de su polinomio minimal)

(¿dos matrices semejantes tienen el mismo polinomio mínimal?)

(proposición 44: A = C.B.C^-1 ⟹ A^k = C.B^k.C^-1 )
(lema 45: si A ∼ B ⟹ P(A) = 0 = P(B) )
(proposición 46: si A ∼ B ⟹ mA = mB )

(polinomio mínimal de una transformación lineal)

(def 47: polinomio minimal de f; notación: m_f o m_{|f|_B} )

(¿también cumplirá que los autovalores de una matriz A son la raíces de su polinomio minimal?)

(proposición 48)

(polinomio mínimal de un vector)

(def 49: P anula a V ⟺ P(v) = 0 )
(proposición 50: para todo vector existe un polinomio mónico que lo anula)
(def 51: polinomio minimal de v; notación m_v)
(ejm 52, 53)

(¿cómo calcular el polinomio mínimal de un vector?)

(proposición 54)

(¿cómo calcular el polinomio minimal con una matriz AeKnxn a partir de los polinomios minimales de los vectores de una base de Kn?)

(proposición 55)
(ejm 56)

(teorema de Hamilton-Cayley (THC))

(teorea 57: teorema de Hamilton-Cayley)
(proposición 58: propiedades del polinomio mínimal de una matriz)

(¿cómo utilizar el THC para calcular las potencias de una matriz?)

(ejm 59)

(el THC en el cálculo de la inversa de A)

(proposición 60)

(un criterio de diagonalización usando el polinomio mínimal)

(proposición 61)
(obs 62)
(proposición 63)
(ejm 64)
(obs 65)
()

(forma de Jordan)
(transformaciones lineales nilpotentes)
(definiciones básicas y propiedades)

(def 1: endomorfismo nilpotente)
(def 2: matriz nilpotente)
(proposición 3: propiedad de una TL nilpotente)
(ejm 4)
(def 5: índice de nilpotencia de una TL)
(def 6: índice de nilpotencia de una matriz)
(lema 7: propiedad de TL nilpontete)
(obs 8)
(proposición 9)
(def 10)
(proposición 11)

(existencia de la forma de Jordan para una TL nilpotente)

(def 12: bloque de Jordan nilpotente)
(lema 13)

(¿será posible encontrar una base de V donde la matriz de f este formada únicamente por bloques de Jordan nilpotentes ubicados en la diagonal y ceros en los demás lugares?)

(teorema 14)
(def 15: forma de Jordan nilpotente)
(def 16: base de Jordan)
(teorema 17)
(def 18: base de Jordan para una matriz)
(ejm 19)

(unicidad de la forma Jordan nilpotente)

(lema 20: J_mxm es un bloque de Jordan nilpotente ⟹ rg(Jⁱ) = m−i )
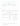
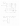
(proposición 21: b_i = rg(Aⁱ) − rg(Aⁱ⁺¹) )
(corolario 22)
(ejm 23)
(lema 24: J y J' son nilpotentes y J∼J' ⟹ J=J' )
(teorema 25: f es TL nilpotente ⟹ |f|_B=J )
(teorema 26)

(caso general)

(caso: forma de Jordan de un endomorfismo cuyo polinomio minimal tiene una única raíz)

(def 26: bloque de Jordan asociado al autovalor lamda de tamaño n)
(lema 27)
(def 28: matriz de Jordan o forma de Jordan)
(teorema 29)
(def 30: base de Jordan de una TL)
(obs 31)
(teorema 32)
(def 33: base de Jordan de una matriz)
(ejm 34)

(unicidad de forma Jordan)

(teorema 35: unidad de la forma de Jordan)
(teorema 36)

(aplicación: cálculo de las potencias de una matriz)

(cálculo de la potencia de una matriz diagonizable)

(obs)
(ejm)

(cálculo de la potencia de una matriz que no es diagonizable)

(ejm)

()

(diagonalización)

(autovalores y autovectores)

(polinomio característico)

(polinomio característico de un endomorfismo)

(una caracterización de matrices diagonizables)

(espacios de autovectores y diagonalización)

(¿cuales son las condiciones suficientes y necesarias sobre los subespacios E, asociados a los autovalores n de A, para que A sea diagonizable?)(teorema 33)

(ejm 34)

(polinomio minimales)

(polinomio minimal de una transformación lineal)

(polinomio minimal de un vector)

(¿cómo calcular el polinomio minimal?)

(teorema de Hamilton-Caley)

(¿cómo utilizar el THC para calcular las potencias de una matriz?)

(el THC en el cálculo de la inversa de A)

(un criterio de diagonalización usando el polinomio minomial)

(forma de Jordan)

(transformaciones lineales nilpotentes)(definiciones básicas y propiedades)

(existencia de la forma de Jordan para una TL nilpotente)

(¿será posible encontrar una base de V donde la matriz de f este formada únicamente por bloques de Jordan nilpotentes ubicados en la diagonal y ceros en los demás lugares?)

(ejm 19)

(unicidad de la forma Jordan nilpotente)(lema 20)

(proposición 21)

(corolario 22)

(ejm 23)

(lema 24)

(teorema 25, 26)

(caso general)

(def 26)

(ejm 34)

(unicidad de forma Jordan)

(teorema 36)

(aplicación: cálculo de las potencias de una matriz)

(cálculo de la potencia de una matriz que no es diagonizable)

No hay comentarios.:

Publicar un comentario

Suscribirse a: Comentarios de la entrada (Atom)