Yachakaj: APLICACIONES DE LAS DERIVADAS Y POLINOMIO DE TAYLOR (teoría + problemas)

miércoles, 24 de noviembre de 2021

APLICACIONES DE LAS DERIVADAS Y POLINOMIO DE TAYLOR (teoría + problemas)

(razón de cambio)

(def 1: rcp y rci)(ejm)(ejm)(ejercicio)(EF)(EF)(PC)(PD)(PD)(PD)(PD)

(teorema de Rolle)

(teorema 1: teorema de Rolle)(ejm)(ejm)(EF)(PC)(PD)(PD)
(ejm 1, 2, 3, 4, 5, 6, 7, 8, 9), (ejm 1, 2, 3, 4), (ejm 1, 2, 3)

(teorema del valor intermedio)

(teorema 2: teorema del valor intermedio de Lagrange)(ejm)
(teorema 3: teorema del valor generalizado)
(ejm 1, 2, 3, 4), (ejm 1, 2, 3, 4, 5), (ejm 1)
(EF)(PC)(PC)(PC)(PC)

(corolarios del teorema del valor medio)

(corolario 1)
(corolario 2)

(teorema del valor medio generalizado)

(teorema 1: teorema del valor medio generalizado)

(teorema (primera regla de L'Hospital, forma 0/0 ))

(teorema 2: primera regla de L'Hospital, forma 0/0 )
(corolario 3)
(corolario 4)

(teorema (segunda regla de L'Hospital, forma ∞/∞))

(teorema 3: segunda regla de L'Hospital, forma ∞/∞)(ejm)

(funciones monótonas)

(recordando)

(def 1)

(condiciones suficiente para monotonicidad de funciones)

(teorema 4: teorema de la derivada y monotonía)(ejm)
(EF)(EF)(EF)(EF)

(valores extremos de una función)

(def 1: máximos y mínimos relativos o locales)(PC)(EF)(EF)(PC)
(teorema 1: relación entre la derivada y valores extremos)(EF)
(teorema 2: Fermat)(def 2: punto crítico)(ejm)
(PC)(PC)(PC)

(funciones convexas y cóncavas en el plano)

(def 3: función convexa)
(def 4: función cóncava)
(teorema 3)(obs)
(PC)(PC)

(máximos y mínimos)

(teorema 1: funciones convexas y cóncavas)(ejemplos)
(teorema 2. criterio de la primera derivada para extremos)(PC)
(método para hallar máximos y mínimos absolutos)(ejm)
(ES)(EF)(PC)(PC)(EF)(PC)(ES)
(ejm 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26)

(punto de inflexión)

(def 1: punto de inflexión; teorema 3)
(PC)(PC)(PC)
(ejm 27, 28, 29, 30, 31, 32)

(criterio de la segunda derivada)

(teorema 4: criterio de la segunda derivada)(PC)(PC)(PC)

(probs)

(asíntotas, gráficas)(ef)(pc)
(máx min)

(funciones inversas y sus derivadas)

(teorema 1)(funciones inversas)
(teorema 2)
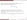
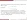
(teorema 3)(ejm)
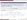
(teorema 4)(ejm)
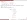
(PC)(PC)(PC)(PC)

(funciones trigonométricas inversas)

(introducción)
(función seno inverso)
(función coseno inverso)
(función tangente inverso)
(funciones cot, sec, csc inverso)

(derivada de inversas)

(introducción)
(funciones hiperbólicas)
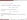
(derivadas de las funciones hiperbólicas)
(funciones hiperbólicas inversas)
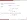
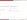
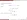
(PC)(EF)(PC)(PC)

(gráfica de funciones)

(ejm)(ejm)

(polinomio de Taylor)

(introducción)(ejm)
(def 1: polinomio de Taylor)(ejm)
(teorema 1: fórmula de Taylor)
(teorema 2: caracterización de Taylor)(ejm)(ejm)
(polinomio de Taylor de una composición)(ejm)
(EF)(PD)(PD)(EF)

(fórmula de Taylor con resto de Lagrange)

(teorema 1: fórmula de Taylor con resto de Lagrange)(ejm)(ejm)(ejm)(ejm)(ejercicio)

()

//(teoremas)

(teorema 1: de Rolle, demostración)(ejm)(ejm)
(teorema 2: del valor medio (Lagrange), demostración)(ejm)(ejm)

(teorema 3: generalizado del valor medio (Cauchy), demostración)

(corolario 1, demostración)
(corolario 2, demostración)
(probs)////

(teorema 4: L'Hopital (forma 0/0))(demostración)

(corolario 3)
(corolario 4)(demostración)
(probs)
(probs)

(teorema 5: L'Hopital (forma ∞/∞))

(probs)

(Ejemplos de L'Hopital)(ejm)(ejm)(ejm)(ejm)
(def 1: función monótona)(ejm)

(teorema 6: condiciones suficiente para que una función sea creciente(decreciente) sobre un intervalo)(ejm)(ejm)

(recordando L'Hopital)(recordando Monotonia)
(derivada y monotonía)

(valores extremos de una función: máximo y mínimo relativos o locales)(gráfico)//

(teorema: derivada y valores extremos)//

asd

(teorema de Fermat; def: punto crítico)(ejm)(obs)

(teorema de Fermat: máximo y mínimos)(ejm)
(def: punto crítico)
asd

(funciones convexas y cóncavas en el plano)

(def: convexa)(def: cóncava)
(teorema: cóncava y convexa)
(teorema: f ''>0 convexa y f ''<0 concava )(ejms)

(teorema 1: criterio de la primera derivada: máximo y mínimo en Xo)//(recordando)(obs)(ejm)

asd

(teorema 2: máximo y mínimo absoluto)(ejm)

(ejm)(ejm)

(def: punto de inflexión, ejm)

asd

(teorema 3: f es dos veces derivable y tiene PI, ejm)(ejm)(ejm)(ejm)
(probs)
(probs profe)

(criterio de la segunda derivada: máximo y mínimo locales)(ejm)//

asd
(probs)

(funciones monótonas)
(aplicaciones de máximo mínimos)
(concavidad y puntos de inflexión)(ptos. de inflexión)
(concavidad)
(traza de gráfico)
(asíntotas, pc, pi, gráfica)
(mazimizar)

(función inversa)

(teorema 1, demostración)
(teorema 2, demostración)(obs)
(teorema 3, demostración)(obs)
(teorema 4)(demostración)(obs)
(teorema 5, demostración)(obs: aplicación)
(probs)

(profe)

(funciones trigonométricas inversas)

(función arcsen)
(función arccos)
(función arctan)
(funciones arccot, arcsec, arccsc)

(derivación de funciones trigonométricas inversas)

(derivada de arccos)
(tabla de las derivadas de funciones trigonométricas inversas)

(funciones hiperbólicas)

(derivada de senh)
(derivada de cosh)
(tabla de las derivadas de funciones hiperbólicas)

(funciones hiperbólicas inversas)

(dominio, rango y gráfica de senh^-1 y cosh^-1)
(senh^-1)
(cosh^-1)
(tabla resumen de las funciones hiperbólicas inversas)
(derivada del senh^-1)
(tabla de las derivadas de las funciones hiperbólicas inversas)
(probs)

(profe)
(probs con implícitas)

(polinomio de Taylor)

(polinomio de Taylor)(orden 2)(ejm)(ejm)

ASD

(definición: polinomio de orden n de f alrededor de Xo)(ejm)
(teorema: fórmula de Taylor infinitesimal)

(¿existirá otro polinomio...?)
(¿qué relación hay entre...?)

(teorema: caracterización del polinomio de Taylor)(ejm)(ejm)
(polinomio de Taylor de una composición)(ejm)

(importancia del residuo)

(teorema: fórmula de Taylor con resto de Lagrange)(ejm)(ejm)

(aplicaciones al cálculo de límites)(ejm)(ejm)(ejercicios propuestos)
(probs)

(polinomio de aproximación)
(cota superior)

No hay comentarios.:

Publicar un comentario

Suscribirse a: Comentarios de la entrada (Atom)