Matrices y determinantes (teoría + problemas)
- (suma de matrices)

- (producto de una matriz y un escalar)


- (multiplicación de matrices)



- (potencia de una matriz cuadrada)

- (matrices conmutables)

- (propiedades de matriz triangular superior)

- (propiedades de matriz triangular inferior)

- (propiedades de matriz simétrica)

- (propiedades de matriz antisimétrica)

- (teorema)

- (matriz idempotente)

- (matriz involutiva)

- (matriz nilpotente)

- (matriz ortogonal)
 (propiedades de a traza y transpuesta)
(propiedades de a traza y transpuesta) (prob)
(prob)
- (matriz invertible)

- (propiedades)
 (prob)
(prob)
- (cálculo de la inversa de una matriz)

- (método de Gauss)
 (ejm)
(ejm)
- (matriz elemental)
 (ejm)
(ejm)
- (teorema)
 (ejm)
(ejm)
- (teoremas)

- (teorema)

- (matrices equivalentes)

- (obs)

- (referencias)

- (motivación)


- (matriz)

- (obs 1, 2)
 (ejm)
(ejm)
- (generación de matrices mediante reglas)
 (ejm)
(ejm)
- (igualdad)
 (ejm)
(ejm)
- (tipos)
- (matriz nula)

- (matriz cuadrada)

- (nota: diagonal principal)

- (traza de una matriz)

- (tipos de matrices cuadradas)
- (matriz diagonal)

- (matriz escalar)

- (matriz identidad)

- (matriz triangular inferior)

- (matriz triangular superior)

- (transpuesta de una matriz)

- (matriz simétrica)

- (matriz antisimétrica)

- (matriz fila)

- (matriz columna)
 (ejm)
(ejm)
- (propiedades)
 (ejm)
(ejm)
- (operaciones)
- (suma de matrices)

- (producto de una matriz y un escalar)

- (propiedades)

- (multiplicación de matrices)
 (ejm)
(ejm)
- (propiedades)

- (probs)


- (definiciones de matrices cuadradas)
- (potencia de una matriz cuadrada)

- (conmutables, teorema)

- (propiedades de matriz triangular superior)

- (propiedades de matriz triangular inferior)

- (propiedades de matriz simétrica)

- (propiedades de matriz antisimétrica)

- (teorema)

- (m. idempotente)

- (m. involutiva)

- (m. nilpotente)

- (m. ortogonal)

- (propiedades de la traza y transpuesta)
 (ejm)
(ejm)
- (probs)

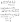
- (probs)

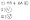


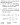
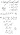

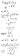
- (probs: vof).


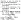
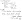
- (probs).

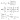
- (matriz invertible)

- (propiedades)
 (problema)
(problema)
- (probs)

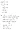
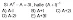


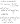

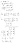

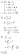
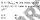
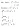

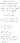




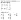








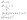
- (cálculo de la inversa de una matriz)
- (operaciones elementales por filas)

- (método Gauss)
 (ejm)
(ejm)
- (probs)
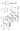

- (matriz elemental)
 (ejm)
(ejm)
- (teorema)
 (ejm)
(ejm)
- (teorema)

- (teorema)

- (equivalentes por filas)

- (equivalentes por columnas)

- (matrices equivalentes)

- (referencias)

- (función determinante)
 (ejm)
(ejm)
- (def recursiva)

- (orden 1)

- (orden 2)

- (orden 3: Sarrus)

- (propiedades)







- (Vandermonde)

- (menor de un elemento)

- (cofactor de un elemento)

- (definición de un determinante según el desarrollo de Laplace)
 (ejm)
(ejm) (ejm)
(ejm)
- (otras propiedades)


- (método práctico: pivot)
 (ejm)
(ejm) (ejm)
(ejm)
- (matriz singular y no singular)
 (ejm)
(ejm)
- (propiedad)

- (adjunta)

 (ejm)
(ejm)
- Introducción a la teoría de matrices.
- Matrices, definición, igualdad.
- Tipos de matrices:
Cuadrada, nula, diagonal, escalar, identidad, triangular superior, triangular inferior,
transpuesta, simétrica, antisimétrica.
- Operaciones con matrices: adición, sustracción y multiplicación.
- Matrices y
operaciones elementales. Definición de matriz invertible y sus propiedades.
- Matrices
equivalentes
- Determinantes.
- Función determinante. (
 )
) - La adjunta y sus propiedades. Cálculo de la inversa de una matriz por cofactores o adjunta. (
 )
)















- Matrices semejantes
-
Introducción a la teoría de matrices.

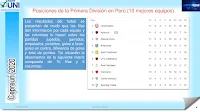

- Matrices, definición, igualdad.





- Tipos de matrices:
Cuadrada, nula, diagonal, escalar, identidad, triangular superior, triangular inferior,
transpuesta, simétrica, antisimétrica. Propiedades.











- Operaciones con matrices: adición, sustracción y multiplicación. Propiedades.






- suma.



- sustracción.
- multiplicación.



- potencia.
- idempotente.
- involutiva.
- nilpotente.
- invertible.
- Matrices y
operaciones elementales.
- Definición de matriz invertible y sus propiedades.





- (matriz elemental).





- Matrices
equivalentes.


- Determinantes. Función determinante. Propiedades.





























- La adjunta y sus propiedades.





- Cálculo de la inversa de una matriz por cofactores o adjunta.







- Matrices semejantes.




















 (propiedades de a traza y transpuesta)
(propiedades de a traza y transpuesta) (prob)
(prob)


 (ejm)
(ejm)




 (ejm)
(ejm)
 (ejm)
(ejm)











 (ejm)
(ejm)
 (ejm)
(ejm)










 (ejm)
(ejm)

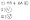


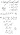

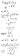


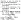
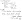


 (ejm)
(ejm)
 (ejm)
(ejm)






 (ejm)
(ejm)


 (ejm)
(ejm) (ejm)
(ejm)


 (ejm)
(ejm) (ejm)
(ejm)
 (ejm)
(ejm)

 (ejm)
(ejm)
 )
) )
)


































































































No hay comentarios.:
Publicar un comentario