- ********************* 2025-2 *********************
(formas multilineales)
- (ejm)
- (teorema: única y existencia)
- (ejm)
- (def)
- (obs)(obs)(ejm)
- (proposición: antisímetrica)
- (proposición)(proposición)(ejm)
- (corolario)(preposición)(ejm 1, 2)
- ()
- (determinante de una transformación lineal)
- (proposición)(propiedades)(obs)
- ()
- (teorema)(corolario)(corolario)(obs)
- (determinante de matrices)
- (def: matriz de orden n)
- (corolario)(corolario)(corolario)
- (regla de Cramer)
- (obs 1)(obs 2)(ejm 1)(ejm 2)
- (proposición)
- (proposición: expansión de Laplace)
- (teorema: determinante en bloques)
- (def: menor de una matriz)
- (proposición: desarrollo de la determinante de una matriz)
- (def: adjunta de una matriz)
- (proposición: matriz invertible)(obs)
- ()
- ///////////////////////////////////////////////////////////////////
- /////////////////////////// 2024-1 ///////////////////////////
- //////////////////////////////////////////////////////////////////
- (formas multilineales)
- (permutación)
- (corolario)(def: alternadas)(teorema)(corolario)(ejm)
- (propiedades)(ejm)
- (teorema)(corolario)
- (alternadas)
- (corolario)(teorema)
- (corolario)
- (obs)(ejm)
- (pullback)
- (propiedades)(teorema)(corolario)
- (pullback)
- (corolario)(teorema)
- ()(corolario)(def)(ejm)(propiedades)
- (determinante de una TL)(teorema)
- ----------------------------------------------------------------------------
- --------------------------------- 2023-2 ---------------------------------
- ----------------------------------------------------------------------------
- (fma)(PC3)
//
//
(EP)
//
//
(PC4)
- (matrices)(PC3)
(EP)
(EF)
- (deteminante)(PC3)
//
(EP)
(PC4)
//
- (PC3)
(PC4)
- (producto interno)(PC4)
- (base ortonormal)(EF)
(pc4)
- (G-S)(EF)
(ES)
(PC4)
- (ortogonalidad)(PC4)
(EF)
(ES)
- (proyeccion)(PC4)
(EF)
- (reisz)(PC4)
- (determinantes)
- (funciones multilineales alternadas)
- (notación)
- (def 1: función multilineal alternada)
(PC3)
- (ejm 2)
- (propiedades básicas de funciones multilineales alternadas)
- (proposición 3)
- (caracterización de las funciones multilineales alternadas)
- (ejm 4)
- (existencia y unicidad del determinante)
- (lema 5: relación entre una fma en K(n+1)x(n+1) y fma's en Knxn)
- (ejm 6)
- (ejm 7)
- (teorema 8)
- (def 9: determinante de orden n)
- (obs 10)
- (corolario 11: desarrollo del determinante por la 1ra columna y por la 1ra fila)
- (ejm 12)
- (determinante de la traspuesta de una matriz)
- (proposición 13: si A ∈ K(nxn) ⟹ |A| = |AT| )
- (ejm 14)
- (propiedades del determinante)
- (proposición 14: si A es de orden n ⟹ |kA| = kn.|A| )
- (matrices triangulares)
- (proposición 16: si A es triangular sup. o inf. ⟹ |A| = Π aii )
- (obs 17)
- (ejm 18)
- (desarrollo del determinante por una fila o columna arbitraria)
- (proposición 19: si A es cuadrada ⟹ |A| = Σ (-1)i+j.aij.|A(i|j)| )
- (ejm 20)
- (determinante del producto de matrices)
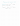
- (proposición 21: si A y B son cuadradas ⟹ |AB| = |A|.|B| )
- (determinantes y matrices inversibles)
- (inversibilidad de matrices)
- (proposición 22: si A es inversible ⟹ |A| ≠ 0 )
- (adjunta de una matriz)
- (def: adjunta de una matriz)
- (ejm 23)
- (proposición 24: si |A| ≠ 0 ⟹ A-1 = adj(A) / |A| )
- (regla de Cramer)
- (proposición 25)
- (ejm 26)
- (rango de una matriz y determinante)
- (def 27: submatriz de A en K(rxs) )
- (ejm 28)
- (proposición 29, 30)
- (----------------------------------------------------------------)
(funciones multilineales alternadas)
(propiedades básicas de fma)
(caracterización de las fma)
(existencia y unicidad)
(determinante de la traspuesta de una matriz)
(ejm 14)
(propiedades del determinante)
(matrices triangulares)
(ejm 18)
(desarrollo del determinante por una fila o columna arbitraria)
(determinante del producto de matrices)
(determinantes y matrices inversibles)(inversibilidad de matrices)
(adjunta de una matriz)
(regla de Cramer)
(rango de una matriz y determinante)
(funciones multilineales alternadas)
(propiedades básicas de funciones multilineales alternadas)
(caracterización de las funciones multilineales alternadas)
(existencia y unicidad del determinante)
(determinante de la traspuesta de una matriz)
No hay comentarios.:
Publicar un comentario