2022-2:
2022-1:
2021-2:
2020-2:
(teorema fundamental del álgebra) (teorema de Bolzano o del valor intermedio)
(teorema de Bolzano o del valor intermedio)

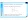
 (otras formas)
(otras formas) (Regla de signos de Descartes)
(Regla de signos de Descartes)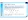
 (teorema: Cardano-Viette)
(teorema: Cardano-Viette)
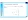
(teorema de la raíces racionales de Gauss)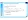
 (raíces imaginarias de un polinomio)
(raíces imaginarias de un polinomio) (raíces irracionales de un polinomio)
(raíces irracionales de un polinomio)




2018-1:
(funciones) (función real de variable real)
(función real de variable real) (funciones elementales)
(funciones elementales) (función cuadrática)
(función cuadrática) (función signo)
(función signo) (máximo entero)
(máximo entero)


 (álgebra de funciones)
(álgebra de funciones) (función par)
(función par) (función impar)
(función impar)
 (función monótona)
(función monótona)

 (función sobreyectiva)
(función sobreyectiva) (función inyectiva)
(función inyectiva) (función biyectiva)
(función biyectiva) (función acotada)
(función acotada) (graficación)
(graficación) (composición)
(composición)
 (imagen y preimagen)
(imagen y preimagen) (función inversa)
(función inversa)
 //(función par e impar, raíz cuadrática y cúbica, valor absoluto, recíproco)
//(función par e impar, raíz cuadrática y cúbica, valor absoluto, recíproco) //(función par e impar)
//(función par e impar) //(biyectiva y acotada)
//(biyectiva y acotada) //
//
 //
//

- Funciones.
- Definición, dominio y rango.
- Propiedades.
- Representación gráfica.
- Funciones elementales: constante, lineal, afín, identidad.
- Funciones reales de una variable real.
- Función cuadrática, cúbica, valor absoluto, raíz cuadrada, función signo y función máximo entero.
- Aplicaciones.
- Tipos de funciones: función par, impar, inyectiva, sobreyectiva, biyectiva.
- Funciones monótonas, homogéneas y funciones acotadas.
- Operaciones con funciones reales: adición, sustracción, multiplicación, división y composición.
- La composición y los tipos de funciones.
- Imagen, Preimagen y propiedades.
- Técnicas de graficación.
- A partir de la gráfica de f, obtener la gráfica de: y = ± f(± x + a) + b, y = f(|x|), y =|f(x)|, y=a f(x), y=f(ax).
- La inversa de una función.
- Definición a partir de la composición.
- Condición necesaria y suficiente de su existencia, Propiedades.
- Dominio y rango de la inversa.
- Determinación de las funciones inversas gráficamente.
No hay comentarios.:
Publicar un comentario